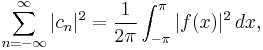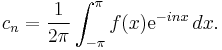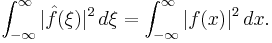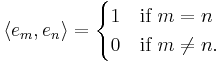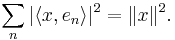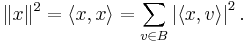Parseval's identity

In mathematical analysis, Parseval's identity is a fundamental result on the summability of the Fourier series of a function. Geometrically, it is the Pythagorean theorem for inner-product spaces.

Informally, the identity asserts that the sum of the squares of the Fourier coefficients of a function is equal to the integral of the square of the function,

$\sum_{n=-\infty}^\infty |c_n|^2 = \frac{1}{2\pi}\int_{-\pi}^\pi |f(x)|^2 \, dx,$

where the Fourier coefficients c_n of ƒ are given by

$c_n = \frac{1}{2\pi}\int_{-\pi}^{\pi} f(x) \mathrm{e}^{-inx} \, dx.$

More formally, the result holds as stated provided ƒ is square-integrable or, more generally, in L²[−π,π]. A similar result is the Plancherel theorem, which asserts that the integral of the square of the Fourier transform of a function is equal to the integral of the square of the function itself. In one-dimension, for ƒ ∈ L²(R),

$\int_{-\infty}^\infty |\hat{f}(\xi)|^2\,d\xi = \int_{-\infty}^\infty |f(x)|^2\, dx.$

Generalization of the Pythagorean theorem

The identity is related to the Pythagorean theorem in the more general setting of a separable Hilbert space as follows. Suppose that H is a Hilbert space with inner product 〈•,•〉. Let (e_n) be an orthonormal basis of H; i.e., the linear span of the e_n is dense in H, and the e_n are mutually orthonormal:

$\langle e_m, e_n\rangle = \begin{cases}1&\mbox{if}\ m=n\\ 0&\mbox{if}\ m \not= n.\end{cases}$

Then Parseval's identity asserts that for every x ∈ H,

$\sum_n |\langle x, e_n\rangle|^2 = \|x\|^2.$

This is directly analogous to the Pythagorean theorem, which asserts that the sum of the squares of the components of a vector in an orthonormal basis is equal to the squared length of the vector. One can recover the Fourier series version of Parseval's identity by letting H be the Hilbert space L²[−π,π], and setting e_n = e^−inx for n ∈ Z.

More generally, Parseval's identity holds in any inner-product space, not just separable Hilbert spaces. Thus suppose that H is an inner-product space. Let B be an orthonormal basis of H; i.e., an orthonormal set which is total in the sense that the linear span of B is dense in H. Then

$\|x\|^2=\langle x,x\rangle=\sum_{v\in B}\left|\langle x,v\rangle\right|^2.$

The assumption that B is total is necessary for the validity of the identity. If B is not total, then the equality in Parseval's identity must be replaced by ≥, yielding Bessel's inequality. This general form of Parseval's identity can be proved using the Riesz–Fischer theorem.

References

Johnson, Lee W.; Riess, R. Dean (1982), Numerical Analysis (2nd ed.), Reading, Mass.: Addison-Wesley, ISBN 0-201-10392-3 .
Titchmarsh, E (1939), The Theory of Functions (2nd ed.), Oxford University Press .
Zygmund, Antoni (1968), Trigonometric series (2nd ed.), Cambridge University Press (published 1988), ISBN 978-0521358859 .

Parseval's identity

Generalization of the Pythagorean theorem

See also

References